Automaticity is the ability to do things without occupying the mind with the low-level details required, allowing it to become an automatic response pattern or habit. It is usually the result of learning, repetition, and practice.
We all know that learning, repetition, and practice are required to succeed on a standardized test, but these tests are complex. Learning, repetition, and practice worked for counting, adding three-digit numbers with carrying, your multiplication table, and picking the right verb for a certain subject, but it might be unclear what automatic skills will apply to the GMAT, GRE, ACT, or SAT.
Our MATHFACTors are designed precisely for this purpose – to develope automaticity that will pay off on what on the GMAT GRE, ACT, or SAT, but you may need some convincing.
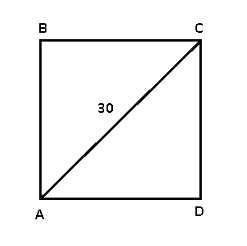
The diagonal of square ABCD is 30. What is the approximate perimeter of the square?
(A) 60 (B) 85 (C) 120 (D) 155 (E) 200
Let’s take a look at how different students might approach this question:
Student 1
After some thought, Student 1 realizes that the diagonal cuts the square into two right triangles. He knows what to do with right triangles – … and has to be whatever the long side is called. No numbers, so he labels the sides AD = [math]x[/math] and CD =[math]y[/math] . Now we get
\(x^2 + y^2 = 30^2\)
Hmmm. What is \(30^2\)? Anyway, two variables one equation… can’t solve an equation with two variables, right? Read the question again. Stare at equation. Read the question again. Wait! It’s a square! So both sides are \(x\) . Now he gets
\(x^2 + x^2 = 30^2\)
Calculate \(30^2\) … So now
\(2x^2 = 900\)
\(x^2 = 450\)
\(\sqrt{450}\)
What? Square root of 450? Okay, gotta prime factor to reduce that root:
\(450 = {2}\times{3^2}\times{5^2}\)
\(\sqrt{450} = {3}\times{5}\times{\sqrt{2}}\)
\(\sqrt{450} = 15\sqrt{2}\)
What? Square root of 2?
Even supposing that Student 1 gets to this point, it’s taken at least three minutes (possibly 5) and it’s high time to guess and move on.
Student 2
Student 2 knows that triangle ABC is a 45:45:90 triangle. The ratio of the sides is
\(x : x : x\sqrt{2}\)
So she can set \(30\) equal to \(x\sqrt{2}\)
\(30 = x\sqrt{2}\)
\(x = \frac{30}{\sqrt{2}}\)
She recalls from the depths of her somewhat shaky memory that \(\sqrt{2}\) is approximately \(1.4\) Now it’s time to break out the calculator, unless she’s taking the GMAT… when it’s time for a nasty calculation.
Thirty seconds later, assuming no mistakes, she gets \(21.42\)
What? That’s not an answer! She checks her calculation. Reads the question again; checks her calculation again; reads the question slowly and carefully. Aha! Perimeter. So \({21.42}\times{4}\) is \(85.71\). She’s not sure about that decimal remainder, but she’s worried about time and answers B.
Maybe less than two minutes. Maybe.
Student 3
Student 3 gets to the nasty calculation almost automatically. He goes straight to an expression for the perimeter before he begins to calculate and do a little trick with exponents.
\(P = \frac{{4}\times{30}}{\sqrt{2}} = {{2^{2}}\times{30}}\times{2^{\frac{1}{2}}}\)
It looks a bit convoluted, but automaticity and pattern recognition lead to this kind of thinking. In the end he gets
\(P = {2 \sqrt{2}}\times{30} = {2 \sqrt{2}}\times{30} = 60\sqrt{2}\)
So the perimeter is approximately \({60}\times{1.4}\) which is \(84\), and the closest answer is B.
Definitely under two minutes, but we can do even better.
Solution 4
Student 4 reads through the problem, including the answers, and the first thing that strikes her is that the difference between the answers is rather large. It’s an approximation problem and given the spread in the answer choices she can be very liberal with her approximation.
The side of the square is definitely less than 30 and more than 15 – the Pythagorean theorem isn’t \(a + b = c\). Therefore
\({4}\times {15}\) < P < \(
[latex]60\) < P < \(120\)
Only one answer satisfies this inequality: B.
This is the essence of efficiency, and it’s a result of automticity. It will take less than a minute. This is the sort of thing that will give you the time you need to answer the really tricky questions.